(Authors: Andres Adjimann and Hartwig Mayer)
Introduction
The security of your crypto-assets depends on one piece of information that you must protect: your private key. If your private key is stolen, all your assets can be stolen. If your private key is lost, all your assets are lost.
You can opt for a custody service which secures your private key. This is a convenient solution, but bears its own risks – starting with the fact that you depend on the response of this institution to access your funds. If you prefer to be your own custodian, you can make use of hardware wallets which store your private key in specialized secure hardware. Some mobile apps use the secure storage on your phone to protect your private key. Nevertheless, if you lose your hardware wallet or your mobile phone (together with the seed phrase to recover your private key), your crypto-assets are gone.
The risk of losing your private key can be greatly reduced by means of a simple idea: use more than one key to sign a transaction. A “multi-layer” policy can be used to protect the private key by, for example, requiring three out of five signatures to successfully sign a transaction. In this case, someone who wants to steal your assets would need at least three of your keys, and, on the other hand, your assets are not lost as long as you do not lose more than two keys. If you lose just one or two keys, a recovery mechanism might be in place which helps you to “restore” your keys.
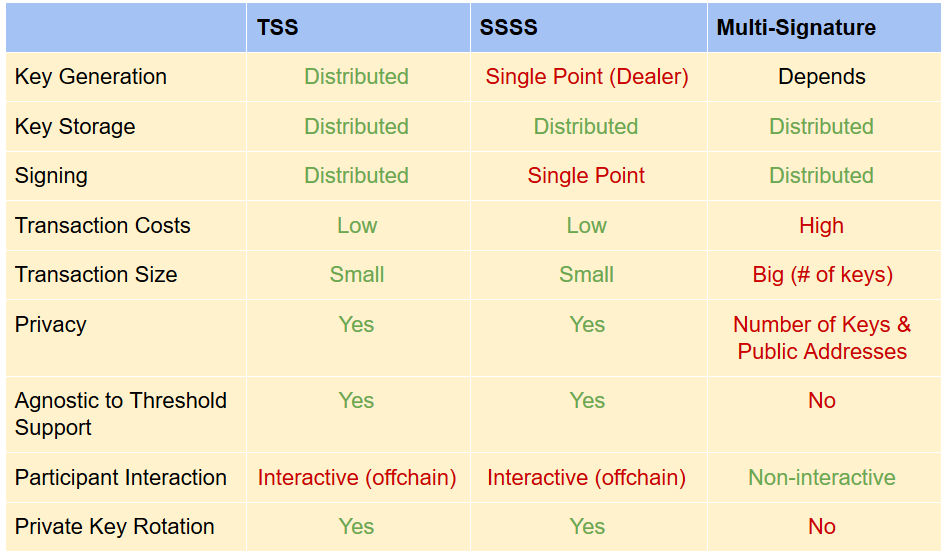
There are different ways to implement this multi-layer policy: multi-signatures, Shamir secret sharing schemes (SSSS), and threshold signature schemes (TSS). Threshold signature schemes have been improved lately, and can now be used for blockchain applications. This solution has several advantages over the other two options. We will compare the three strategies, discuss their pros and cons, and describe the way TSS is used in the ZenGo wallet.
Threshold Signature Schemes
Threshold signatures are a special kind of public key cryptography. Instead of deriving the public key from a single private key, in threshold signatures each participating party has its own secret share and must jointly calculate the group public key. Hence, there is no single private key anymore, and the risk associated with its custody is distributed.
Threshold signature schemes are composed of three algorithms, like the single key signature scheme, but reflect the more complex logic of having more players involved: there are n players and 0 <= t+1 <= n are needed to sign a transaction, while t parties fail to successfully sign. The protocol is split into three steps:
- Key Generation: all players receive the same public key and a secret share of the private key.
- Signing: An input of a transaction and at least t+1 out of n shares outputs a valid signature.
- Signature Verification: This algorithm works the same way as in the single key signature scheme, i.e., it takes the public key and the signature as input and produces “ok” as output only when the signature is correct.
TSS solutions and implementations are available for ECDSA, Schnorr, and BLS signing algorithms (see for example ZenGo or the TSSKit). Each implementation faces specific challenges. ECDSA is the most difficult to modify to enable the use of a threshold protocol. Unfortunately, most major blockchains, including Bitcoin and Ethereum, only support ECDSA. But there are solutions for this, too!
Some Major Challenges
A – Distributed Key: There must never be more than one secret share in plain format at a single location in any phase of the protocol:
- Distributed Key Generation: The protocol must avoid a “dealer” who distributes the secret shares, since this would mean having all shares in a single location.
- Distributed Signing: The protocol must provide a valid signature for a transaction by using the secret shares, but without joining the shares to rebuild the signing key.
B – Malicious Participants: Since you have to run the protocol with other parties, this opens the door to malicious participants, who might, for example, try a rogue public-key attack (see here on page 3) for signature malleability. To avoid such problems, all parties must prove their compliance with the protocol.
C – Protocol Complexity: The protocol must solve the above mentioned challenges, while being efficient enough to be practical. Recent research proposes solutions which generate, sign and verify ECDSA threshold signatures in milliseconds.
Where does the complexity enter?
C.1 Distributed key generation must simulate a dealer by running several secret sharing protocols, or may make use of homomorphic encryption which increases the complexity of the protocol.
C.2 Schnorr and BLS are linear signature schemes, i.e. the signature is just the sum of the individually signed transaction by each party which uses it secret share. In ECDSA we are faced with the problem (see here for an explanation) that the signature is not linear, and extra protocol communication is required to reduce it to the linear case.
C.3 Signature schemes can be reused to sign many transactions with the same public and private key pair. ECDSA and Schnorr schemes require for each new signature a random nonce, otherwise the private key can be deduced from a previous signature. To produce this random nonce, it is required for every signature to run a similar protocol to distributed key generation.
Other Multi-Party Signatures
Multi-Signatures
Multi-signatures are implemented in the blockchain as a smart contract or, in the case of Bitcoin as a special OP code. The contract contains a list of n public keys along with some number 0 < t+1 <= n for the threshold. The blockchain does not accept a transaction if it is signed by less or equal to t keys.
Advantages of multi-signatures:
- they are not interactive, which saves the trouble of running a complex off-chain communication between the different signers, once the multi-signature contract is setup.
Disadvantages of multi-signatures:
- they are blockchain specific and have to meet the blockchain specifications
- transactions are recognizable by their special format
- they leak information about number of signers and their public keys
- they have a bigger transaction size and cost
- communication should be handled off-chain and they are not standardized
Shamir Secret Sharing Schemes
Shamir secret sharing is a cryptographic strategy in which one private key is split into shares, and t+1 out of n shares are needed to reconstruct it. After key reconstruction, the transaction is signed as in the single key case.
Advantages of SSSS:
- it avoids all disadvantages of multi-signatures
Disadvantages of SSSS:
- a “dealer” generates the private key secret shares in a single location
- parties must reconstruct the full private key in order to sign, resulting in a single point of failure
Both TSS-based and SSSS-based wallets have the advantage of allowing proactive secret sharing, i.e., private key rotation: the secret shares can be used to generate a new set of secret shares which work for the same public key! Players delete their old shares, so a repeat attacker does not gain an advantage. This makes TSS and SSSS-based wallets more secure in the long term.
ZenGo Mobile Wallet
Threshold wallets have the promise to provide a convenient and secure Key Management System (KMS) that frees the user from the private key custody worries and allows comprehensive control mechanisms without the trade-off of handing over the access rights to a third party.
The ZenGo Mobile wallet is based on a 2 out of 2 threshold signature model: one share is stored on your mobile device and the other in the ZenGo server. If one of the shares is compromised, your assets are still safe. But what about full control over access to your funds? Since the threshold is set to 2, a mechanism for key recovery becomes necessary. There are two cases to be considered:
Self-Recovery: In case you lose your secret share, a classical backup mechanism is in place: half of your key is stored at the service provider and the other half is stored in your iCloud. (Note that threshold wallets cannot easily provide an HD structure for key recovery, but requires another multi-party protocol to introduce a distributed HD structure).
Counterparty Recovery: This is the case when ZenGo gets hacked or their server does not respond anymore. In the present implementation this is resolved by using an escrow mechanism with trusted third party services (Escrow and Trustee). Trustee is monitoring ZenGo services, and Escrow provides the second share of ZenGo, in case Trustee asks for it. More info in their blog post.
The development team of ZenGo has a very interesting crypto solution to the Counterparty Recovery problem on their roadmap: TMOVE Protocol. This replaces the third party services, but requires more than one secret share holder (see this video for more information).
Since threshold wallets are blockchain agnostic, ZenGo could react quickly to be the first wallet after Calibra to support the Libra test network and already succeeded to support the Tezos network without using the smart contracting functionality (which required an implementation over the Ed25519 curve).
We want to thank Omer Shlomovits from ZenGo (by KZen) for providing us with very valuable feedback on our article.
Source Code
References
[GG18] Fast Multiparty Threshold ECDSA with Fast TrustlessSetup.
[BDN18] Compact Multi-Signatures for Smaller Blockchains
[L17] Fast Secure Two-Party ECDSA Signing
[CCLST19] Two-Party ECDSA from Hash Proof Systems andEfficient Instantiations
[DKLS18] Secure Two-party Threshold ECDSA from ECDSA Assumptions
Interesting blog posts:
Threshold Signatures in ChainLink












